Правила умножения дробей: простых, смешанных, десятичных
Математика: правила умножения дробей
Переходя из начальной школы в среднюю, учащиеся на уроках математики изучают простые и десятичные дроби и вычисления, связанные с ними. Сложение и вычитание простых дробей требуют приведения их к одному знаменателю, затем производятся математические действия с дробями с одинаковыми знаменателями. Мы будем рассматривать деление и умножение дробей.
Умножение простых дробей
Умножение дробей — пожалуй, самое простое из вычислений, связанных с дробями. Правила несложные, и решение не должно вызвать затруднений. Умножение обыкновенных дробей входит в программу математики за 5 класс.
Умножаем простые дроби
Если требуется найти произведение двух простых дробей, нужно перемножить числители и записать результат в числитель ответа, затем перемножить знаменатели и результат записать в знаменатель:
({{7}over{8}}×{{2}over{5}}={{14}over{40}})
Эту дробь можно сократить, получим ({{7}over{20}}).
Видео «Сокращение дробей»
Иногда школьники задают вопрос: как производить умножение дробей с разными знаменателями. При необходимости умножить одну дробь на другую не имеет значения – с одинаковыми они или с разными знаменателями. А вот попытаться максимально сократить числа до вычислений и после них – желательно. Это ускорит решение.
Для сокращения нужно попробовать разложить числа на простые множители:
12 = 2 х 2 х 3;
15 = 5 х 3.
Четные числа можно сократить, разделив на 2. После сокращения чисел вычисления будет производить легче:
Важно! При необходимости перемножить более трех дробей порядок действий будет таким же: перемножаются все числители, результат записывается в числитель, перемножаются все знаменатели – результат записывается в знаменатель.
Для решения задач с обыкновенными дробями можно пользоваться переместительным и сочетательным свойствами умножения. Это позволяет упростить решение сложных примеров с несколькими множителями, переставив их местами, расставив скобки, что позволит сократить дроби.
Пример
({{2}over{9}}×{{12}over{18}})
сократим ({{12}over{18}}={{2}over{3}})
решаем ({{2}over{9}}×{{2}over{3}}={{2×2}over{9×3}}={{4}over{27}})
Умножение неправильных дробей производится так же, после вычисления при возможности лучше провести сокращение дроби.
Умножаем простую дробь на натуральное число
Если один множитель — простая дробь, а другой — целое число, числитель умножается на это число, а знаменатель остается без изменения. Объяснение простое: любое натуральное число можно записать в виде дроби:
5 = ({{5}over{1}});
Поэтому запись вычисления будет выглядеть так:
({{3}over{8}}×4)= ({{3}over{8}}×{{4}over{1}} = {{12}over{8}} ={{3}over{2}}).
Из неправильной дроби выделим целую часть: ({{3}over{2}}) = 1 ({{1}over{2}})
Умножаем простую дробь на смешанную
Если необходимо перемножить простую дробь на смешанную, вторую нужно превратить в неправильную и произвести вычисления по приведенному выше правилу:
({{3}over{5}}×1{{1}over{3}}) = ({{3}over{5}} ×{{4}over{3}} = {{12}over{15}}).
Сокращаем дробь:
({{12}over{15}}) = ({{4}over{5}}).
Умножаем смешанную дробь на смешанную
Такие примеры решаются по тому же принципу: обе дроби превращают в неправильные, перемножают и сокращают:
1 ({{1}over{5}}) х 2 ({{1}over{3}}) = ({{6}over{5}}) х ({{7}over{3}}) = ({{42}over{15}}) = ({{14}over{5}}) = 2 ({{4}over{5}}).
Видео «Правила умножения дробей»
Умножаем обратные дроби
Обратными называют дроби, у которых числитель первой дроби равен знаменателю второго, а знаменатель первой дроби равен числителю второй:
Примеры:
({{4}over{5}}) и ({{5}over{4}});
При перемножении между собой взаимно обратных дробей результат будет равен единице.
Действительно, ({{4}over{5}} ×{{5}over{4}}={{4 × 5}over{5 × 4}} = {{20}over{20}}) = 1.
Умножение отрицательных дробей
Эта тема может вызывать трудности, поэтому важно запомнить следующие правила:
«минус» на «минус» дает «плюс»;
«минус» на «плюс» дает «минус».
Поэтому до проведения операций с числами нужно «разобраться» со знаками, вынеся их за границы умножения. Если в итоге всех действий останется один «минус», ответом будет отрицательное число, если все «минусы» сократятся – положительное.
Умножение десятичных дробей
Операции с умножением десятичных дробей можно произвести двумя способами:
— Представив десятичную дробь в виде простой:
0,25 х 2,5 = ({{25}over{100}}) х ({{250}over{100}}) = ({{625}over{1000}}).
Умножение десятичных дробей входит в программу математики за 6 класс. Кажущиеся сложными примеры, когда один множитель — десятичная дробь, а другой — обыкновенная, сводятся к тому, что их нужно привести к одному виду – к которому проще:
0,25 × ({{3}over{4}}) = ({{25}over{100}}) × ({{3}over{4}}) = ({{3}over{16}});
Разберем подробнее:
Десятичную дробь 0,25 представили в виде обыкновенной дроби ({{25}over{100}}), сократив ее на 25 получим дробь ({{1}over{4}})
затем умножаем ({{1}over{4}}×{{3}over{4}}={{1×3}over{4×4}})
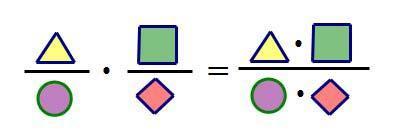
Правила умножения дробей можно записать в виде формулы:
({{a}over{b}}) x ({{c}over{d}}) = ({{a × c}over{b × d}}).

Правила умножения дробей
Понимать правила умножения дробей важно еще и потому, что деление их сводится тоже к действию умножения: при необходимости разделить обыкновенную дробь на обыкновенную, делимое станет первым множителем, а второй множитель — дробь, обратная делителю:
({{5}over{9}}):({{1}over{3}})=({{5}over{9}}) × ({{3}over{1}}) = ({{15}over{9}}) = ({{5}over{3}})
Преобразуем 1({{2}over{3}}).
При умножении и делении дробей нужно быть очень внимательными при записи, особенно при сокращении и вычислениях. Не ленитесь записать лишнее промежуточное вычисление: лучше потратить на запись несколько минут, чем, ошибившись, пересчитывать все вновь.



